Übungen

Anmeldung
Prozedere
Übungstermine
Übungsblätter
Zusatzmaterial

Anmeldung

Flow Chart zur OLAT Anmeldung

Die Verwaltung der Übungsgruppen findet in OLAT statt.
Die Anmeldung ist von Mo 27.10., 16:30 Uhr bis Fr 31.10., 20:00 Uhr freigeschaltet.

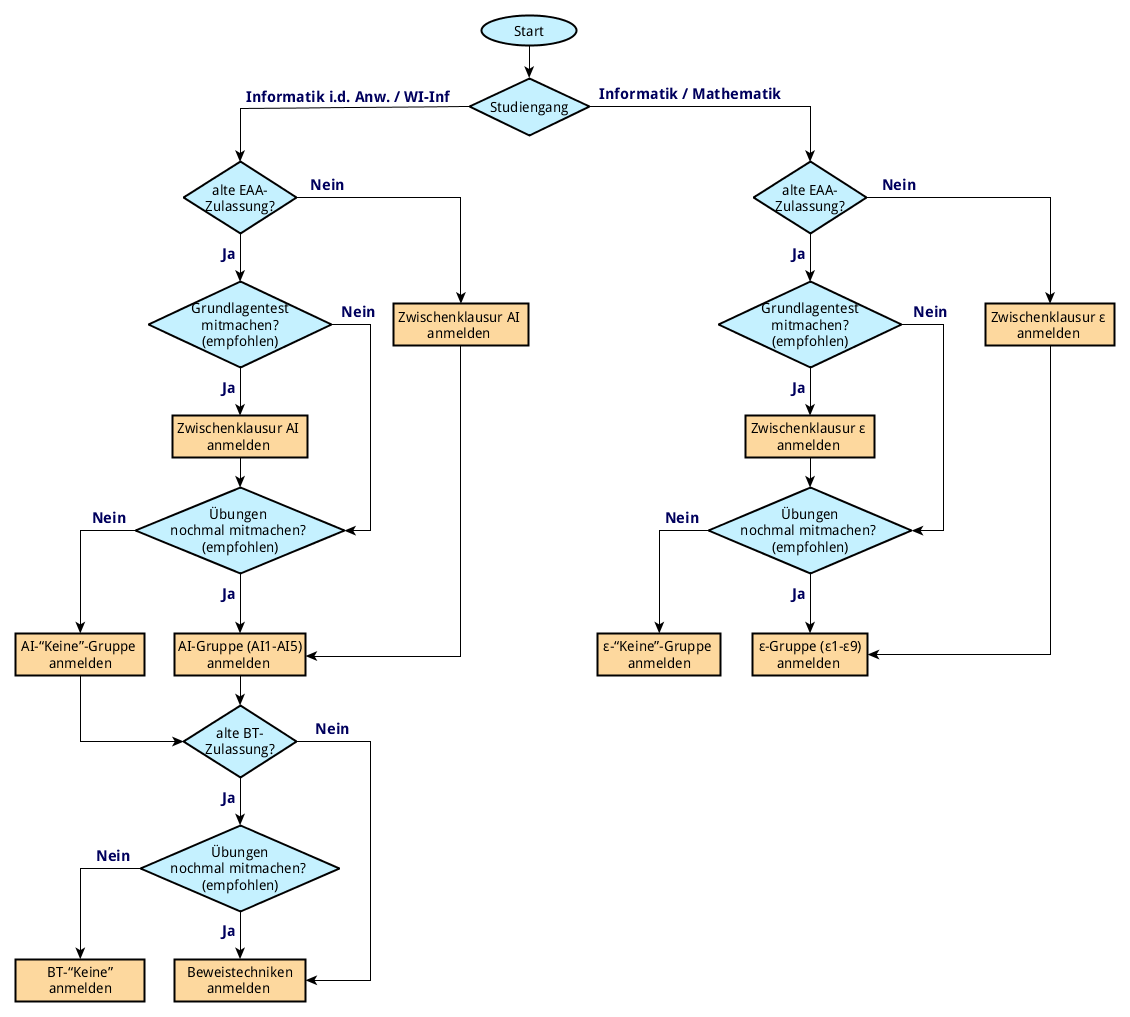
Achtung: Eine Anmeldung (im richtigen Track) ist unbedingt nötig, wenn eine Zulassung erworben werden soll! Teilnehmer aus dem Track AI, die noch nicht die Beweistechniken bestanden haben, melden sich hierfür bitte zusätzlich an.

Hinweis: Melden Sie sich bitte auch an, wenn Sie nicht am Übungsbetrieb teilnehmen möchten, etwa weil Sie die Zulassung schon früher erworben haben; wir haben hierfür Pseudogruppen "Keine" vorgesehen. Dies erleichtert uns die Verwaltung eben dieser vorhandenen Zulassungen und Ihnen die Prüfung, um Missverständnisse und Fehler zu vermeiden.

Prozedere

Die Auswahl der Übungs- und Klausuraufgaben richtet sich nach dem belegten Modul. Hierfür teilen wir die Teilnehmerschaft in Track ε (Inf, Math) und Track AI (AI, WII) ein; Studenten aus anderen Studiengängen halten bitte mit uns Rücksprache. Bitte achten Sie unbedingt darauf, die richtigen Übungen zu besuchen!

Details zur Organisation von Übungen und den extraordinären Terminen in den ersten drei Wochen finden Sie in den Folien aus der ersten Vorlesung (für Ausnahmen und Zusatztermine siehe auch der Kalender im KIS (Vorlesung, Übung)).

Die genauen Zulassungsvoraussetzungen finden Sie hier.

Termine

Die Übungstermine sind: (Achtung: Die Termine im KIS sind nicht korrekt/aktuell.)

Gruppe	Tutor	Tag	Zeit	Raum
ε1	Jan Bormann	Dienstag	08:15	46-654
ε2	Jan Bormann	Dienstag	11:45	46-268
ε3	David Deininger	Mittwoch	10:00	48-462
ε4	Johannes Freiermuth	Mittwoch	13:45	48-280
ε5	Jakob Wenzel	Donnerstag	08:15	48-379
ε6	David Deininger	Donnerstag	10:00	13-370
ε7	Jakob Wenzel	Donnerstag	11:45	13-305
ε8	Johannes Freiermuth	Donnerstag	11:45	56-230
ε9	Timo Ußner	Donnerstag	15:30	48-654
AI1	Florian Pelz	Dienstag	10:00	48-654
AI2	Florian Pelz	Mittwoch	08:15	48-654
AI3	Markus Löwenstein	Mittwoch	13:45	57-165
AI4	Markus Löwenstein	Mittwoch	15:30	48-379
AI5	Nico Himpele	Donnerstag	11:45	56-232

Die ersten Übungen starten in KW 45, also ab dem 04. November.

Die Saalübung, in der Lösungen für die Basisaufgaben präsentiert werden, findet dienstags, 15:30 Uhr in Raum 52-207 statt. Der erste Termin ist am 11. November.

Übungsblätter

Die Übungsblätter werden donnerstags in der Vorlesung ausgegeben – Reste liegen im SCI aus – und sind am jeweils übernächsten (Vorlesungszeit-) Freitag fällig. Die genaue Abgabezeit entnehmen Sie bitte dem jeweiligen Übungsblatt.

Die Übungsblätter finden Sie hier (die alten Links sind leider tot).

Blatt 1	Track ε	Track AI
Blatt 2	alle Tracks
Blatt 3	Track ε	Track AI
Blatt 4	alle Tracks
Blatt 5	alle Tracks
Blatt 6	Track ε	Track AI
Blatt 7	alle Tracks
Blatt 8	Track ε	Track AI
Blatt 9	Track ε	Track AI
Blatt 10	alle Tracks
Blatt 11	alle Tracks
Blatt 12	alle Tracks

* Geändert seit Ausgabe in der Vorlesung.

Die Übungsblätter zu Beweistechniken finden Sie auf der entsprechenden Seite.

Zusatzmaterial

Why Generating Functions Rule
Ein kleiner Überblick darüber, wie und warum Erzeugendenfunktionen funktionieren. "Lücken" im formal-mathematischen Gefüge werden benannt und Literatur angegeben, in der diese adressiert werden.
Rechenregeln für Grenzwerte von Quotienten
Zum asymptotischen Vergleich von Funktionen bestimmen wir gerne Grenzwerte von Quotienten von Funktionen. Hierfür gibt es einige "Rechenregeln", die zum Teil in unpräziser Form überliefert sind. Einige bieten wir hier in sauber bewiesener Form an. (Bitte teilen Sie uns etwaige Unsauberkeiten mit!)
Self-Deceit Sheet
Dies ist eine in Anlehnung an das TCS Cheat Sheet benannte Sammlung von Fehlern, die in Klausuren gemacht worden sind. (Sie soll nicht der humoristischen Erbauung auf Kosten Anderer dienen, sondern ein Werkzeug zur Klausurvorbereitung sein.)